序文
先月までは、データの関連性を相関係数で把握する手法を学びました。そこで、次に、相関がありそうな2変数のデータを「原因系」と「結果系」の関係でとらえ、それらの関係を「回帰直線」であらわします。その直線の式である「単回帰式:y=a+bx」を求める「単回帰分析」をおこなうことにより2つのデータの関係を数式で記述することができ、「予測」が可能となります。これが回帰分析の醍醐味です。
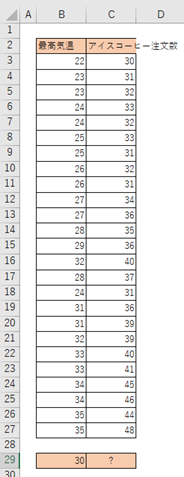
今回は、以下の「最高気温」と「アイスコーヒーの注文数」のデータから、最高気温30℃の時のアイスコーヒーの注文個数を予測していきます。

●単回帰分析とは
・2つのデータ群を「原因系」と「結果系」の関係でとらえ、それらの関係を「回帰直線」であらわす
・得られた回帰直線から「単回帰式:y=a+bx」を求める
●単回帰分析のメリット
・「原因と結果」の関係がありそうな2群のデータの関係を数式で記述することより、データの「予測」ができる
●単回帰分析の注意点
・2つのデータ群の間に「原因系」と「結果系」の関係がありそうな場合、単回帰分析が利用できる
・まず散布図を描き、2変数の相関関係や外れ値などを確認する
・単回帰式を求めたら、式の「精度」を必ず確かめてから予測に用いる
単回帰分析とは
以下のようなデータを得ました。
事例)最高気温とアイスコーヒーの注文個数
●単回帰分析と回帰直線
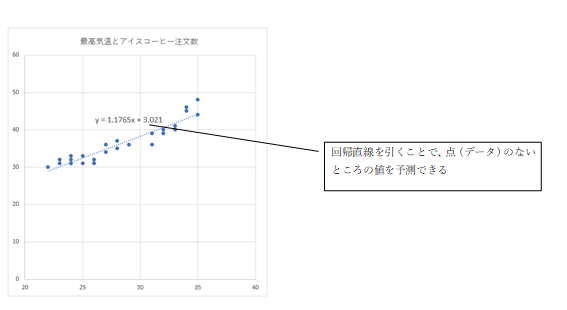
単回帰分析とは、2つのデータ群を「原因」と「結果」の関係でとらえたとき、それらの関係を「回帰直線」で表すことのできる分析手法です。得られた回帰直線から「単回帰式:y=a+bx」を求めることで点(データ)のない部分でも値を予測することが出来るようになります。単回帰式:「y=a+bx」の2変数(xとy)のうち、原因系データであるxのことを「説明変数」といい、結果系データであるyのことを「目的変数」といいます。bはいわゆる直線の傾きを表しますが、統計学では「回帰係数」と呼びます。aは「切片」です。それぞれの値は、後述する「最小二乗法」という数学的考え方にもとづいて求められます。
回帰式を求めて最高気温30℃の時のアイスコーヒーの注文数を予測する
●分析の手順
最高気温とアイスコーヒーの注文数のデータをザッと見てみると、最高気温が上がるに連れてコーヒーの注文数も増加しているようです。つまり、暑くなればなるほどアイスコーヒーが売れるという関係、すなわち前回学んだ「正の相関」がありそうです。また、これらの関係を別の見方で表すなら、「最高気温」という「原因系データ」によって「アイスコーヒーの注文数」という「結果系データ」が変動していると捉えることができます。これらの関係を利用して、最高気温30℃の時のアイスコーヒーの注文数を予測します。
① 2変数のデータの因果関係(どちらが「原因系」で、どちらが「結果系」なのか)を把握します。
② 2変数のデータの関係を散布図や相関係数で確認し、単回帰式を求めることの妥当性をチェックします。
③ 単回帰式(y=a+bx)を求めます。
④ 単回帰式の精度を確認します。
⑤ 単回帰式に値を代入し、予測します。
それでは、ここから実際の分析を行っていきます。
単回帰分析を行う大前提として、2群のデータの間に「因果関係(原因系と結果系)」と「相関関係」が必要です!
データを予測したいと思っても、そもそも単回帰分析をおこなう妥当性が無いようなデータでは意味がありません。単回帰分析は、2群のデータの間に「原因と結果」の関係があり、なおかつ「相関」が認められる場合に有効な分析手法です。
まず、2変数データを散布図で視覚化することにより、外れ値等の極端に離れたデータがないかどうかチェックします。また、表を描くときは、「原因となるデータは左の列に、結果となるデータは右の列に」配置します。そうすると、散布図の横軸(x軸)には原因データが、縦軸(y軸)には結果データが表記されますので、続いて単回帰式を求める際にも有効です。
「散布図」は、[挿入]タブの[グラフ]の[散布図]から作成します。
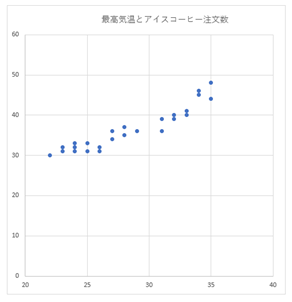
散布図より、外れ値等の異常データが含まれていないことが確認できたので、このまま分析を進めていきます。
「相関係数」を求めます。
CORREL関数を用いる場合、結果を表記させたいセルに
「=CORREL(範囲1, 範囲2)」と入力します。

最高気温とアイスコーヒーの注文数の相関係数は0.94となりました。これより、最高気温と注文数の間には非常に強い相関がありそうなので、これらのデータをもとに単回帰分析をおこなう意義はありそうです。
●ここがポイント
分析したいデータの間に、
①「原因と結果」の関係があるかどうか
②「相関」が認められるかどうか
③外れ値等の異常データが存在しないかどうか
を事前に確認しておくことは、単回帰分析をおこなう大前提として必要不可欠なステップです。これら3つを網羅しないデータに対しては単回帰分析をおこなうと解釈を誤る恐れがあります。確認したデータに不適合な点が認められた場合は、まずは単回帰分析に相応しいデータを準備する作業(データ収集方法の見直しや、既存データの整理等)に取り掛かりましょう。
単回帰式を求める~分析ツールを用いる~
Y=a+bxという単回帰式を求める方法には、散布図から求める方法と分析ツールから求める方法がありますが、今回は分析ツールを使った方法を紹介します。
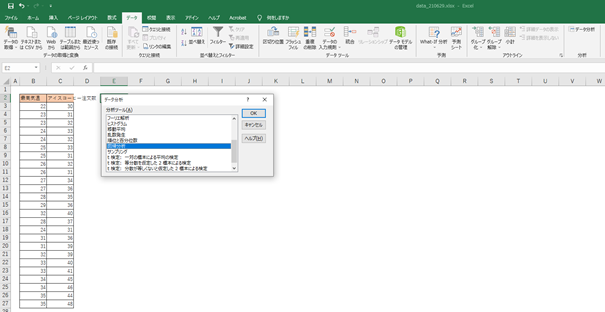
1.[データ]タブの[分析]で[データ分析]を選択します。
2.[分析ツール]の中から[回帰分析]を選びます。
3.[OK]をクリックします。
4.[入力Y範囲]には、「結果系データ」のアイスコーヒーの注文数のデータを選択します。
[入力X範囲]には、「原因系データ」の最高気温のデータを選択します。
このとき、XとY(原因と結果)を間違えないように指定してください。
5.列の先頭にデータのラベル(項目名)がある場合は[ラベル]にチェックを入れます。
6.[OK]をクリックします。
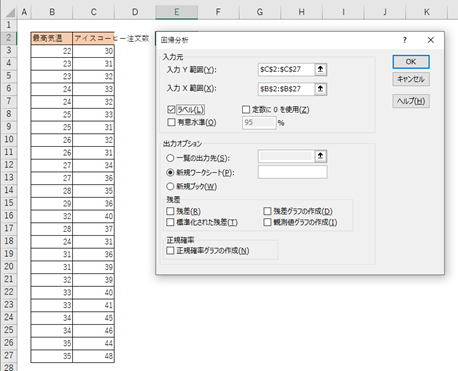
7.出力結果が表示されます。
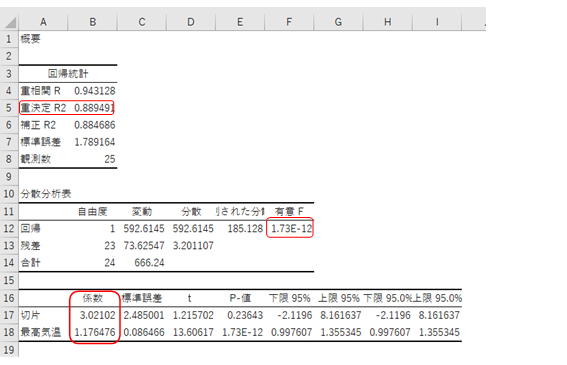
●回帰式の確認
出力結果の左下に示されている数値が、単回帰式:y=a+bxのb(回帰係数)とa(切片)となります。今回の例では、切片は3.02、最高気温の係数は1.18なので、(小数点第2位までで四捨五入しています)
y=3.02+1.18x
という単回帰式が導き出されます。
●回帰関係を求める意義があるかどうか?
回帰分析の結果が出力されたら、まず[分散分析表]にある[有意F]の値を確認します。
有意F=1.73E-12
1.73×10のマイナス12乗なので、ほぼ0に近くなります。この値が、0.05よりも小さければ、母集団についてもこの式が成り立つと仮定してもよいと判断します(=回帰関係の有意性の検討)。あくまでも抽出されたサンプルから得ている式なので、これが母集団についても成り立っていなければ式を求める意義がありませんので、ここの値をしっかり確認しましょう。
●回帰式の精度の確認(寄与率)
散布図や分析ツールから単回帰式が出力されました。しかし、その式をそのまま鵜呑みにするのは危険です。
その式が2つの変数間の関係をどの程度あらわしているかを確かめておく必要があります。
回帰直線の精度の良さ(yの変化を説明変数xでどの程度説明できるか)を判断する基準として一般的に使われているのは単相関係数を2乗した値です。この値は「決定係数」や「寄与率」とも呼ばれ、Excelでは、「重決定R2」と表記されます。R2は0から1の値をとり(0≦R2≦1)、R2が1に近ければ近いほど回帰式の精度が良い(xと yの関係が強い)ことを意味します。
この値が、0.89ということは、アイスコーヒーの注文数の変動は、最高気温という変数で約89%説明がつくということです。単回帰分析では、文字通り説明変数xが1つ(この場合、最高気温)しかありませんので、単相関係数rの2乗が寄与率「重決定R2」と一致します。
●MEMO [回帰分析]の出力結果の「回帰統計」のエリアには、回帰式の当てはまりの良さを判断するための指標が出力されています。

・「重相関R」:一般的に「重相関係数」と呼ばれる統計量であり、この例では単回帰分析(説明変数が1つ)のため(単)相関係数と一致します。
・「重決定 R2」:重相関係数を2乗した値であり、重決定係数と呼ばれる統計量です。データ全体の何%を回帰式によって表現できているかという寄与率をあらわしています。
・「補正 R2」:「自由度調整済み決定係数(自由度調整済み寄与率)」と呼ばれる統計量です。説明変数が複数になった場合の「重回帰分析」ではこの指標をモデルの精度評価に使用します。
・「標準誤差」:回帰式から求められた予測値のバラツキを示す値です。データから回帰式で表現できる部分を除いた「残差」の標準偏差のことですので、この値が小さいほうが式の当てはまりは良いということになります。残差とは、観測された目的変数の値と回帰直線によって求められる予測値とのズレ(誤差)を意味しています。
・「観測数」:データ数を示しています。
単回帰式を用いて最高気温30℃の時のアイスコーヒーの注文数を予測する
いよいよ、アイスコーヒーの注文個数を予測します。
シンプルには、求めた
y=3.02+1.18x
とう回帰式のxに30を代入すればyは求めることができますが、書式上、小数点を四捨五入しているので、より正確に予測値を計算するために、TREND関数を使った求め方を紹介します。
●TREND関数の使い方
=TREND (yの範囲, xの範囲, 予測に使うxの値,定数)
*定数:切片の扱い方を指定します。
TREUEまたは省略→切片を出力する
FALSE→切片を出力しない
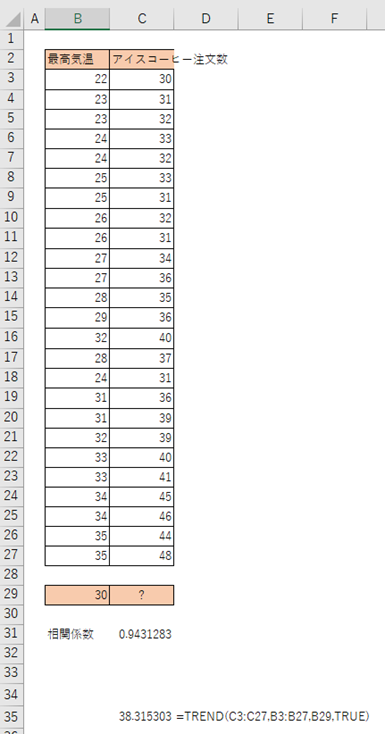
=TREND(C3:C27,B3:B27,B29,TRUE)
最高気温が30度のときは、38.3の注文数が来ると予測できます。
単回帰分析の注意点
最高気温が40℃の時のアイスコーヒーの注文個数は?
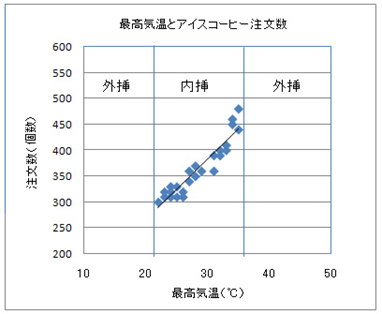
今までの流れで考えると、y=3.02+1.18xのxに40を代入すれば、40℃の時のアイスコーヒーの注文数は予測できそうです。しかし、そう簡単にはいきません。なぜなら、下表を見るとわかるように「最高気温」の最小値は22℃であり、35℃であるため、その範囲内に入っていない40℃を予測することは「外挿」と呼ばれるエリアの予測になってしまい精度が落ちるからです。
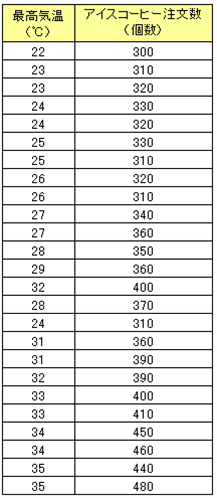
「外挿」はデータの無い範囲(外側)の値を推定することを意味し、その対となるのが「内挿」です。下図を見ても明らかなように、最高気温30℃は内挿であるため、自信をもって予測することができたわけです。しかし、40℃では外挿となってしまうため、単回帰式に代入すれば値そのものは求められますが、残念ながら数学的に信頼することはできないのです。
株価の変動を考えてみてください。急な不祥事や好材料が無いかぎり、明日の株価を予測することは比較的簡単ですが、1ヶ月先や1年先など、予測の範囲が広がれば広がるほど信憑性は薄くなっていきます。同様に、単回帰式を用いた予測においても、既存データの最小値や最大値からかけ離れた値での外挿には注意が必要です。
●MEMO:最小二乗法とは?
Excelでは、単回帰式y=a+bxの回帰係数aと切片bを求めるのに、最小二乗法という計算方法をしています。数式を使わずにイメージだけ紹介すると、以下のようになります。
長方形で囲まれた部分を町に見立てて、プロットの一つ一つを家だと仮定します。今、この町に新幹線を引こうと思ったら、誰からもクレームをこないようにバランスよく5つの家から最短の距離になるように配慮してレールを引くとします。
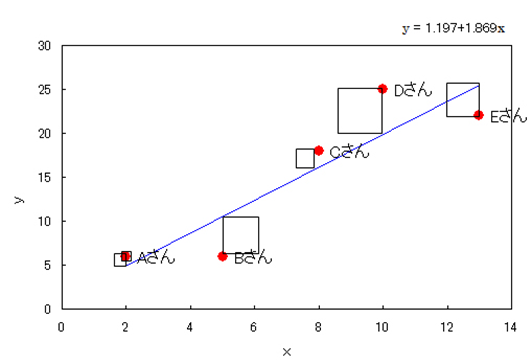
この時、レールのイメージは、y=a+bx+誤差 になります。誤差とは、各家から直線に向かって、縦軸に平行な直線を引いた時の距離になります。この誤差を単純に足し合わせると、プラスとマイナスが相殺されるので二乗します。誤差を二乗することは、正方形の面積を求めることになります。最小二乗法では、この5つの正方形の面積(誤差の二乗和)が最小になるように、傾きb、切片aを求めるものです。
執筆者情報
末吉正成(すえよし・まさなり)
株式会社メディアチャンネル 代表取締役。www.media-ch.com
道具としてのビジネス統計を用いて大学や自治体のWEBコンサルテーションを行う。
著書に『EXCELビジネス統計分析(ビジテク)』(翔泳社)、『EXCELマーケティングリサーチ&データ分析』(翔泳社刊)、『Excelでかんたん統計分析』(オーム社刊)、『事例で学ぶテキストマイニング』(共立出版刊)、『Excelでかんたんデータマイニング』(同友館刊)、『仕事で使える統計解析』(成美堂出版刊)、『見せる統計グラフ』(秀和システム刊)他がある。
ご意見やご感想をお寄せください
データ活用なうでは、今後もより皆さまのデータ利活用に寄与するために、さまざまな専門家の方にその知見を伺い、発信してまいります。
今回の記事がためになった、実務に役に立った方は、ぜひいいね!やシェアをお願いします。
また、筆者の方へご意見・ご感想がありましたら、コメント欄や下記からお問い合わせください。
それでは、次回の記事にもご期待ください!
「ビジネスを成功に導くデータ活用術」連載バックナンバー
今回も前回に引き続き、末吉正成さん「ビジネスを成功に導くデータ活用術」をテーマに執筆いただきました。
データマイニング、データサイエンス、機械学習、AI等々言葉が先行しがちな昨今ですが、時流に流されず、地に足をつけたデータ活用をおこなうための考え方、フレームワーク、そして使い方の注意点などをご紹介いただいております。ぜひご覧下さい。








