序文
複数の変数の間に関係があるかどうかを数値的に表現する方法の一つに相関分析があります。関連性の強さを表す相関係数の求め方と使い方の注意点を紹介します。

相関係数の求め方
世の中には、「身長」と「体重」、「広告のクリック率」と「コンバージョン」、「喫煙率」と「肺がん罹患率」など、その関連性を見たい場合が多くあります。「喫煙率」と「肺がん罹患率」などは、いかにも強く関係していそうですが、それが「どの程度」関係性があるかは、数値化し比較して初めてその強さを知ることができます。この関連の強さを数値で求める手法の一つに「相関分析」があります。今回は、以下の「平均気温」と「ビールの出荷量」のデータを通して、関連性を検証していきます。
コンビニチェーンの店舗マネージャーは、平均気温とビールの出荷量のどんな関係があるかを調べています。以下のデータを得ました。

今回はExcelを用いて解説しますが、RでもPythonでもコードは異なっても考え方は同じですので、適宜自分の分析するツールに置き換えて考えてみてください。
散布図を用いて、データを視覚化する
2列、12行のデータなので、だいたいデータの特色はわかりますが、データを見たら、まずグラフを用いて視覚化することが大切です。
表頭のラベルを含め、C3からD15までを選択した状態で、挿入タブのグラフの中から散布図を選びます。
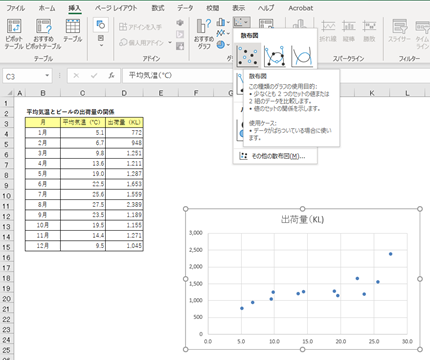
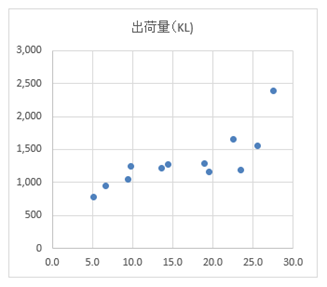
散布図から、平均気温(横軸)が増えるとビールの出荷量(縦軸)が増えている(右上がり)傾向がありそうです。このように一方の値が大きくなると、他方も大きくなる傾向がある関係を正の相関があると表現します。逆に、「シートベルトの着用率」と「車両事故の件数」のように、着用率があがると事故が減る(事実かどうかは不明ですが)ような関係のことを負の相関といいます。
散布図と相関の関係

次に、その相関の強さをもう少し具体的に数値化してみます。以下の式で求められる値を相関係数と呼び関連性の強さを表します。
相関係数は、小文字のr(英語のcorrelationのr)で表します。
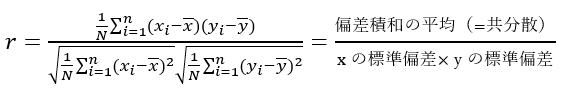
ごく簡単にいうと分子は偏差積の和がどうバラついているかの指標(プラスなのかマイナスなのか)で、分母は、標準偏差で割ることで平均ゼロ、標準偏差1でデータをまとめています。
ここからがより重要です。
rは、常に-1から1の間の値をとります(-1≦r≦1)。相関係数がプラスのときは、正の相関がある(平均気温が上がると出荷量が増えるような関係)といいます。反対に相関係数がマイナスのときは、負の相関がある(失業率が上がると実質経済成長率が下がるような関係)といいます。
●相関の強弱とは?
相関が0.9あったら、相関が強くありそうです。では、0.8の場合はどうでしょうか?これも相関は強そうです。では、0.6の場合は? 0.2の場合は? となってくるとどこまでを持って相関があるといっていいのか迷われるかもしれません。残念ながら統計的に0.5以上は相関ありとする!といった明確な基準はありません。あくまでも目安ですが、以下の表を参考に相関の強弱を判断してください。
| 相関係数(絶対値) | 相関の強さの目安 |
| ~0.3未満 | ほぼ無相関 |
| 0.3~0.5未満 | 非常に弱い相関 |
| 0.5~0.7未満 | 相関がある |
| 0.7~0.9未満 | 強い相関 |
| 0.9以上 | 非常に強い相関 |
実際に相関係数を求める
相関係数の数式を分母、分子で求めなくて、Excelの場合、CORREL関数で求めることができます。求めたいセルに以下の入力をすることで相関係数を求めることができます。
=CORREL(範囲1, 範囲2)
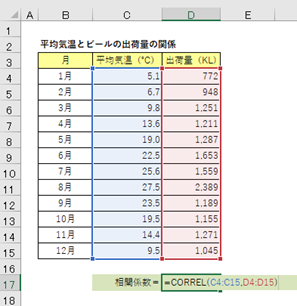
平均気温とビールの出荷量の相関係数は、0.78と強い正の相関があることがわかりました。
見せかけの相関に要注意:相関の落とし穴
2つの観測値があった場合の関連の度合いを相関係数というモノサシで学びました。それでは、以下について、相関係数を考えてみましょう。
変数のXとYの関係を見ています。相関係数は、0.6と計算されます。これは、相関があるといってよいでしょうか?
散布図をかいてみます。
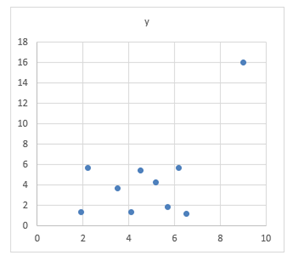
極端に遠くにある値があります。10番目のxが9、yが16というデータです。このように、極端に離れたデータのことを外れ値と呼びます。それでは、この10番目のデータをとって、1から9番までで、散布図を描き、相関係数を求めてみます。
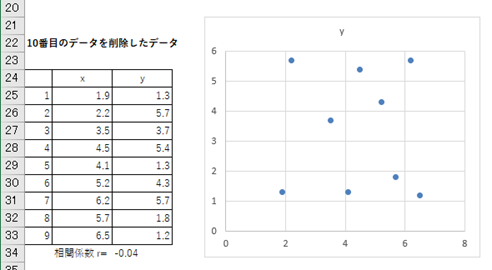
散布図に注目してください。各点がばらばらで、一定の傾向があるデータに見えません。相関係数で確認すると、-0.04となり、相関はなしという評価になります。
もう一つデータを見てみましょう。
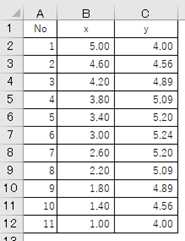
ぱっと見た感じではなにか規則性がありそうですが、数字だけではなんとも分かりづらいので散布図をかいて、相関係数を求めてみましょう。
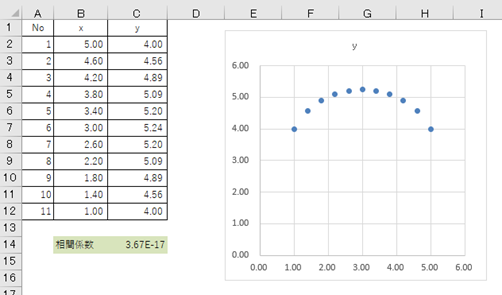
視覚化すると2次曲線の放物線となっており、xとyの間に関係はありそう(接線の傾きが変わるx=3.0付近を境に左右対称に分布)ですが、相関係数の値はゼロになっています。
ちなみに、「E-17」とはどんな意味でしょうか。
xとyの相関が3.67E-17とは、3.67×10のマイナス17乗という意味です。3.67×10のマイナス2乗だと、ゼロの桁が2つ左に移動するので、0.0367になります。3.67E-17は、3.67からコンマの桁が左に17も移動するので、限りなくゼロに近いということになります。Excelでは、このE-○○という表記がよく出てきますので解釈をしっかり覚えておきましょう!
まとめ
- 相関係数は、外れ値の影響を強く受けるので、データを見たら、いきなり相関係数を計算するのではなく、まず視覚化をして、データの特徴(外れ値等がないかどうか)をつかむようにしましょう。
- 相関係数は上述の式の通り、2つのデータの関係を直線(リニア)で表している指標になります。相関係数は2つのデータ群の関連性を表す一つの指標ではありますが、すべての関連性を網羅しているわけではありませんので注意しましょう。
次回の連載は、今回触れなかった相関係数を求める式の意味(あの式は何を意味しているのか? 正の相関の場合、右上がりになるのはなぜ?)をもう少し詳細にみていきますのでお楽しみにしてください。
執筆者情報
末吉正成(すえよし・まさなり)
株式会社メディアチャンネル 代表取締役。www.media-ch.com
道具としてのビジネス統計を用いて大学や自治体のWEBコンサルテーションを行う。
著書に『EXCELビジネス統計分析(ビジテク)』(翔泳社)、『EXCELマーケティングリサーチ&データ分析』(翔泳社刊)、『Excelでかんたん統計分析』(オーム社刊)、『事例で学ぶテキストマイニング』(共立出版刊)、『Excelでかんたんデータマイニング』(同友館刊)、『仕事で使える統計解析』(成美堂出版刊)、『見せる統計グラフ』(秀和システム刊)他がある。
ご意見やご感想をお寄せください
データ活用なうでは、今後もより皆さまのデータ利活用に寄与するために、さまざまな専門家の方にその知見を伺い、発信してまいります。
今回の記事がためになった、実務に役に立った方は、ぜひいいね!やシェアをお願いします。
また、筆者の方へご意見・ご感想がありましたら、コメント欄や下記からお問い合わせください。
それでは、次回の記事にもご期待ください!
「ビジネスを成功に導くデータ活用術」連載バックナンバー
今回も前回に引き続き、末吉正成さん「ビジネスを成功に導くデータ活用術」をテーマに執筆いただきました。
データマイニング、データサイエンス、機械学習、AI等々言葉が先行しがちな昨今ですが、時流に流されず、地に足をつけたデータ活用をおこなうための考え方、フレームワーク、そして使い方の注意点などをご紹介いただいております。ぜひご覧下さい。








