序文
CORREL関数ですぐ解を求める前に、一度、相関係数はどんな計算をもって関係の強さを測っているのか理解する。

相関係数の求め方:式の意味を理解する
前回、コンビニチェーンの平均気温とビールの出荷量のデータを再掲します。
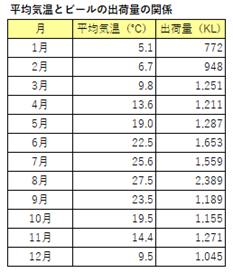
散布図を描いて、データを視覚化します。
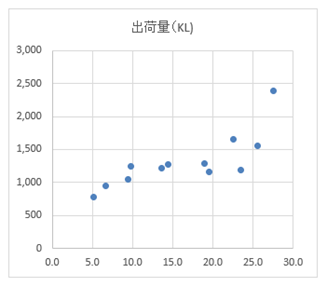
散布図から、平均気温(横軸)が増えるとビールの出荷量(縦軸)が増えている(右上がり)傾向がありそうです。このような関係を正の相関と呼びました。
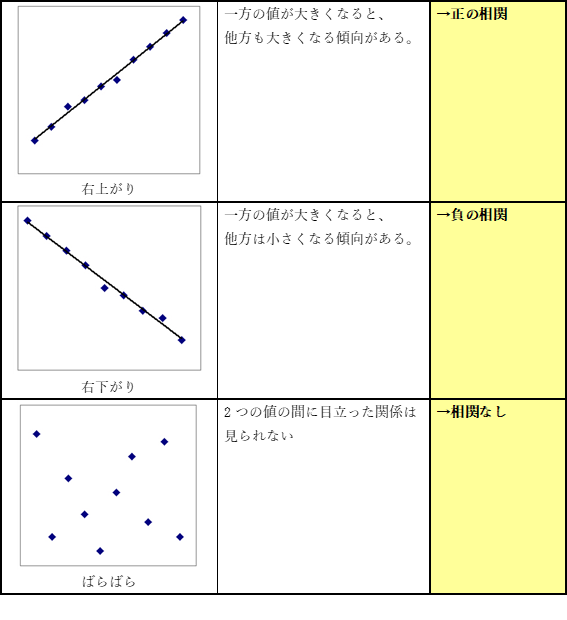
次に、その相関の強さをもう少し具体的に数値化してみます。以下の式で求められる値を相関係数と呼び関連性の強さを表します。
相関係数は、小文字のr(英語のcorrelationのr)で表します。

ごく簡単にいうと分子は偏差積の和がどうばらついているかの指標(プラスなのかマイナスなのか)で、分母は標準偏差で割ることで平均ゼロ、標準偏差1でデータをまとめています。
rは、常に-1から1の間の値をとります。相関係数がプラスのときは、正の相関がある(平均気温が上がると出荷量が増えるような関係)といいます。反対に相関係数がマイナスのときは、負の相関がある(失業率が上がると実質経済成長率が下がるような関係)といいます。
それでは、今回のこの分子と分母が何をやっているのかを解説します。
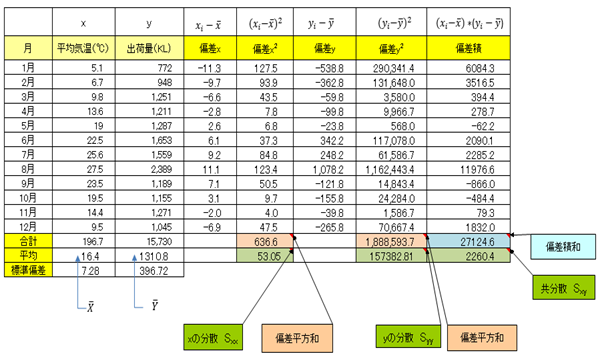
相関係数を計算する過程の表を作成しました。
これから見方を解説します。
平均気温をx、出荷量をyとして、average関数を使って求めます。左からxの各値からxの平均(16.4)を引いた値を計算します。ちなみに、データと平均との差(乖離ともいいます)のことを偏差と呼びます。偏差とはばらつきを示す指標の一つになります。偏差は、英語では、deviationなので、よく聞く標準偏差をSDと書くのは、standard deviationの略になります。
ここで、問題です。
偏差を全部足し合わせるといくつになると思いますか? 偏差を全部足し合わせるとばらつきの大きさを表しているように感じるかもしれません。
答えは、偏差は平均からの乖離なので、足し合わせるとゼロになります。平均よりも大きい偏差であればプラスになり、平均よりも小さい偏差であれば、マイナスになるので、全部の偏差を合計するとゼロになります。これだとばらつきの指標がゼロになってしまうので、指標として使えません。そこで、偏差を2乗することで、プラスマイナスの影響がないようにします。それが、〖〖(x〗_i-x ̅)〗^2の列になります。
偏差の2乗を足し合わせたものを偏差平方和といいます。このままでは、データのばらつきは、データの個数が多いほど、2乗したものを足し合わせると大きくなるので、データの個数で割る必要があります。偏差平方和をデータの個数で割ったものが、一度は聞いたことがあるかもしれませんが、分散と呼ばれるものです。出荷量のyも同様に求めます。
次に、2つの変数の関係を見たいので、2つの変数を1つの組として考えるためにxとyの偏差の積を求めます。この2変数データの組(x,y)の平均を(x ̅ , y ̅ )とすると、平均(x ̅ , y ̅ )から各組の散らばりをしめす(=2組の場合の分散)ことができます。偏差の積を全部足したもの(偏差積和)をデータの個数で割ったものを特に共分散といいます。
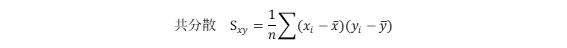
共分散(Sxy)は、2変数の間の正負の関係性を見る便利な統計量ですが、単位の影響を受けたり(例えば身長の単位をcmからmに変えるだけで共分散の値は変わってきます)、複数の共分散の値で関係性を比較できないので、それぞれの変数の分散の平方根をとったもの(=標準偏差)の積で割って標準化(平均0、標準偏差1)してあげるとより相関の強弱が比較しやすくなります。このようにしてできたものが相関係数といいます。式で書くと以下のようになります。
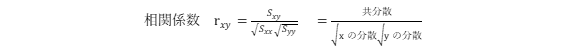
正の相関が右上がりになぜなるのか?:視覚的に理解する
相関係数の式の意味が理解できたとして、次によく聞く質問が、なぜ正の相関だと右上がりなのですか?という質問に視覚的に答えてみたいと思います。
まず最初に出てきた平均気温と出荷量のデータの散布図を確認します。
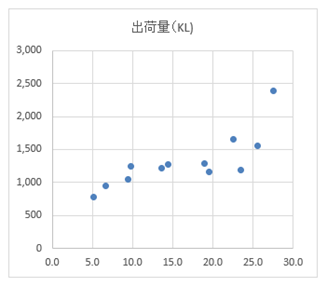
先程の数式の意味を図解で視覚化していきます。
まず、平均気温である16.4度に赤いラインを設けます。当然ながら、平均より大きい個々のデータは、右側にプロットされます。
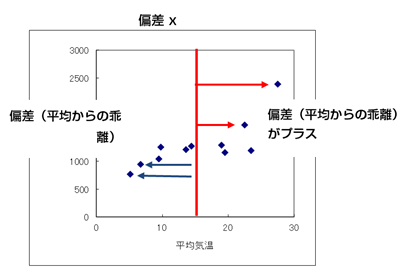
符号としては、平均よりも大きいので偏差はプラスになります。赤い線より左側は、逆に偏差はマイナスになります。出荷量であるyも同様に以下のようにプロットされます。
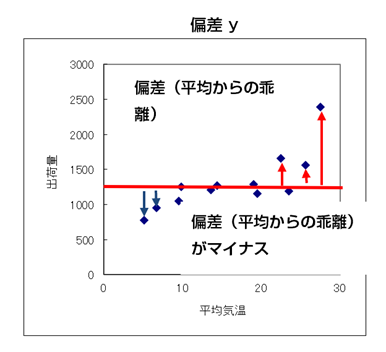
Yである出荷量の平均は1310.8なので、横軸に平均の赤い線を設けます。先程の平均気温であるxと同様に、yの場合は、平均より上の方は偏差がプラスになり、一方で、平均より小さい出荷量は赤線より下にプロットされ符号はマイナスになります。
以下の図のように、xの平均値とyの平均値を散布図上で合わせることで、4つの領域に分けることができます。
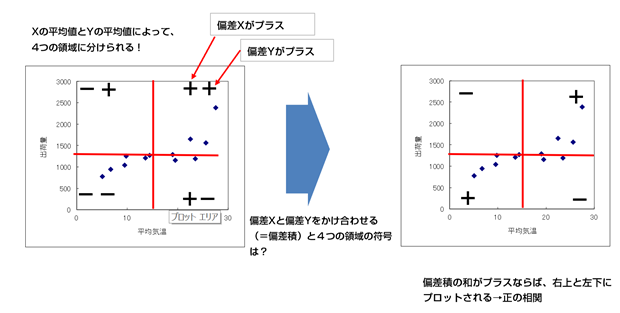
今、2変数間の関係を見ているので、xとyの偏差をかけ合わせます。符号だけに注目すると、例えば、右上のエリアは、xで見ると平均より大きいデータなのでプラス、yの視点で見ると平均より大きいデータなのでプラスなります。ここでは、xとyの積なのでプラスとプラスをかけてもプラスなのでこのエリアはプラスになります。
一方、左上のエリアに注目してください。ここは、xに注目すると、平均より小さいデータが集まっているので符号はマイナスになります。一方でyに注目すると、平均より上側にあるので、こちらはプラスになります。この場合、xとyをかけ合わせるとプラスとマイナスの掛け算なので、符号はマイナスになります。
このような感じで2変数の積を符号に注目してみると、偏差の積をかけ合わせたもの(=偏差積)がプラスであれば、右上と左下にデータがプロットされることになります。これが正の相関が右上がりになる理由です。逆に負の相関は、左上と右下にプロットされるので、右下がりの散布図になります。
いったん、相関係数がどのような理屈で成り立っているのかをしっかり理解したら、次からは、ショートカットして、CORREL関数を使って、すばやく相関係数を求めましょう。もちろん、関数を使う前にデータを視覚化することを忘れないように気をつけてください。
執筆者情報
末吉正成(すえよし・まさなり)
株式会社メディアチャンネル 代表取締役。www.media-ch.com
道具としてのビジネス統計を用いて大学や自治体のWEBコンサルテーションを行う。
著書に『EXCELビジネス統計分析(ビジテク)』(翔泳社)、『EXCELマーケティングリサーチ&データ分析』(翔泳社刊)、『Excelでかんたん統計分析』(オーム社刊)、『事例で学ぶテキストマイニング』(共立出版刊)、『Excelでかんたんデータマイニング』(同友館刊)、『仕事で使える統計解析』(成美堂出版刊)、『見せる統計グラフ』(秀和システム刊)他がある。
ご意見やご感想をお寄せください
データ活用なうでは、今後もより皆さまのデータ利活用に寄与するために、さまざまな専門家の方にその知見を伺い、発信してまいります。
今回の記事がためになった、実務に役に立った方は、ぜひいいね!やシェアをお願いします。
また、筆者の方へご意見・ご感想がありましたら、コメント欄や下記からお問い合わせください。
それでは、次回の記事にもご期待ください!
「ビジネスを成功に導くデータ活用術」連載バックナンバー
今回も前回に引き続き、末吉正成さん「ビジネスを成功に導くデータ活用術」をテーマに執筆いただきました。
データマイニング、データサイエンス、機械学習、AI等々言葉が先行しがちな昨今ですが、時流に流されず、地に足をつけたデータ活用をおこなうための考え方、フレームワーク、そして使い方の注意点などをご紹介いただいております。ぜひご覧下さい。




